Skip to contents

Optimal design with LOQ data in PopED

Optimization with a model for warfarin

Andrew Hooker

Source: vignettes/articles/handling_LOQ.Rmd
handling_LOQ.Rmd

Define a model

Here we define, as an example, a one-compartment pharmacokinetic model with linear absorption (analytic solution) in PopED (Nyberg et al. 2012).

library(PopED)
packageVersion("PopED")
#> [1] '0.7.0'
ff <- function(model_switch,xt,parameters,poped.db){
  with(as.list(parameters),{
    y=xt
    y=(DOSE*KA/(V*(KA-CL/V)))*(exp(-CL/V*xt)-exp(-KA*xt))
    return(list(y=y,poped.db=poped.db))
  })}

Next we define the parameters of this function. DOSEis defined as a covariate (in vector a) so that we can optimize the value later.

sfg <- function(x,a,bpop,b,bocc){
  parameters=c( CL=bpop[1]*exp(b[1]),
                V=bpop[2]*exp(b[2]),
                KA=bpop[3]*exp(b[3]),
                DOSE=a[1])
}

We will use an additive and proportional residual unexplained variability (RUV) model, predefined in PopED as the function feps.add.prop.

Define an initial design and design space

Now we define the model parameter values, the initial design and design space for optimization. We define model parameters similar to the Warfarin example from the software comparison in Nyberg et al. (2015) and an arbitrary design of one group of 32 individuals.

poped_db <- 
  create.poped.database(
    ff_fun=ff,
    fg_fun=sfg,
    fError_fun=feps.add.prop,
    bpop=c(CL=0.15, V=8, KA=1.0), 
    d=c(CL=0.07, V=0.02, KA=0.6), 
    sigma=c(prop=0.01,add=0.25),
    groupsize=32,
    xt=c( 0.5,3,50,120),
    discrete_xt = list(c(0.5,1:120)),
    minxt=0,
    maxxt=120,
    a=70,
    mina=0,
    maxa=100)

Simulation

First it may make sense to check the model and design to make sure we get what we expect when simulating data. Here we plot the model typical value and a 95% prediction interval (PI) for the intial design:

plot_model_prediction(poped_db, model_num_points = 500,facet_scales = "free",PI=T)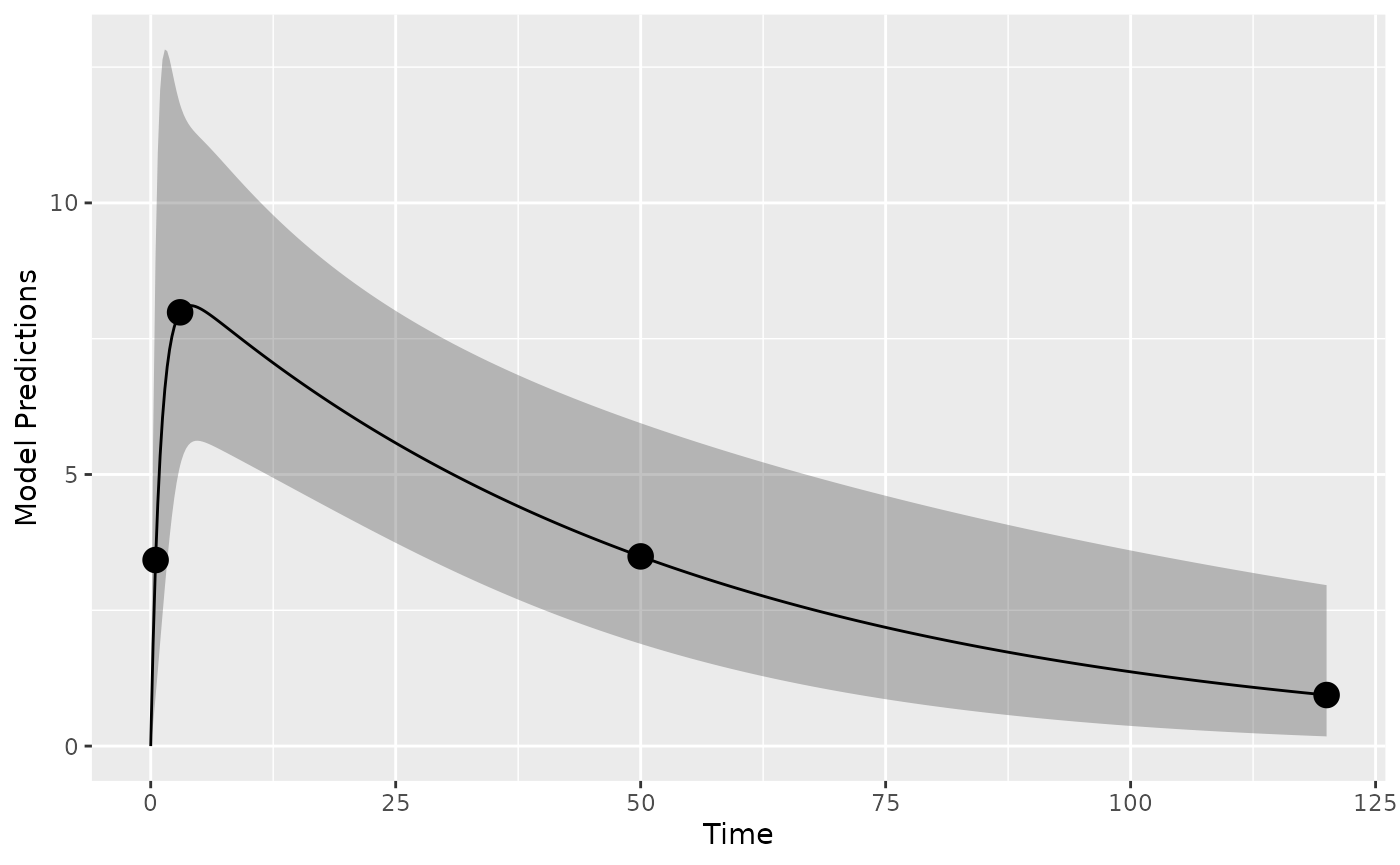

Design evaluation

Next, we evaluate the initial design.

eval_full <- evaluate_design(poped_db)
round(eval_full$rse)
RSE
CL 5
V 4
KA 15
d_CL 34
d_V 70
d_KA 28
sig_prop 89
sig_add 36

We see that the relative standard error of the parameters (in percent) are relatively well estimated with this initial design except for the between subject variability parameter for volume of distribution (d_V) and the proportional RUV parameter (sig_prop).

LOQ handling

We assume that the LOQ level is at 2 concentration units. Here shown as a red dotted line.

library(ggplot2)
plot_model_prediction(poped_db, model_num_points = 500,facet_scales = "free",PI=T) + 
  geom_hline(yintercept = 2,color="red",linetype="dotted",linewidth=1)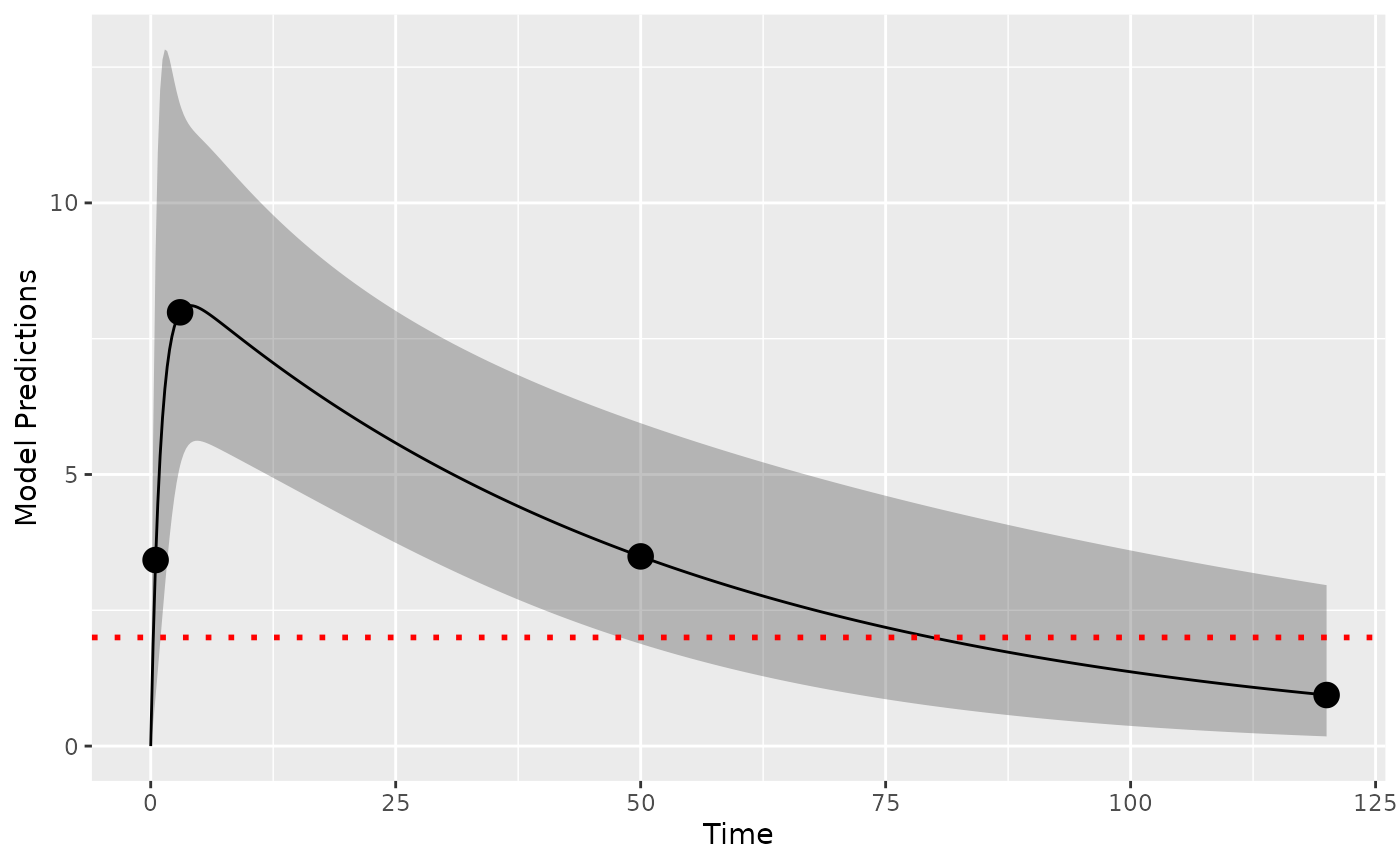

To evaluate the designs we use the design evaluation criteria based on the “integration and FIM scaling” method (loq_method=1 which is the default) and the “omit observations where PRED<LOQ” method (loq_method=2) from Vong et al. (2012) (referred to as the D6 and D2 methods, respectively, in the presentation by Vong et al.). In the D6 method we:

  1. Enumerate all permutations of each sample point being quantifiable or not (below the lower LOQ, or above the upper LOQ). If sample points have an expected prediction interval (default is 95%, loq_PI_conf_level = 0.95) that does not overlap the LOQ then the design point is assumed to either always be observed or to always be outside the limit of quantification.

  2. Compute the probability of each permutation occurring, filtering out potential realized designs with very low probabilities (default is loq_prob_limit = 0.001).

  3. Evalaute the Fisher Information Matrix (FIM) for all remaining design permutations, assuming no information from any design point if, for that permutation, it is not in within the limits of quantification.

  4. Take the weighted sum of the resulting information matrices.

The D2 method is a simplification of this process where all samples with a typical value prediction (PRED) below the lower LOQ or above upper LOQ are removed from the design before calculating the FIM.

Here we evaluate the initial design with both methods and test the speed of the computations. We see that D6 is significantly slower than D2 (but D6 should be a more accurate representation of the RSE expected using M3 estimation methods).

set.seed(1234)
e_time_D6 <- system.time(
  eval_D6 <- evaluate_design(poped_db,loq=2)
)

e_time_D2 <- system.time(
  eval_D2 <- evaluate_design(poped_db,loq=2, loq_method=2)
)

cat("D6 evaluation time: ",e_time_D6[1],"seconds \n" )
cat("D2 evaluation time: ",e_time_D2[1],"deconds \n" )
#> D6 evaluation time:  0.041 seconds 
#> D2 evaluation time:  0.007 deconds

The D2 method is the same as removing the last design point, as you can se below.

poped_db_2 <- create.poped.database(
    ff_fun=ff,
    fg_fun=sfg,
    fError_fun=feps.add.prop,
    bpop=c(CL=0.15, V=8, KA=1.0), 
    d=c(CL=0.07, V=0.02, KA=0.6), 
    sigma=c(prop=0.01,add=0.25),
    groupsize=32,
    xt=c( 0.5,3,50),
    discrete_xt = list(c(0.5,1:120)),
    minxt=0,
    maxxt=120,
    a=70,
    mina=0,
    maxa=100)
eval_red <- evaluate_design(poped_db_2)
testthat::expect_equal(eval_red$ofv,eval_D2$ofv)
testthat::expect_equal(eval_red$rse,eval_D2$rse)

The predicted parameter uncertainty for the three methods is shown in the table below (as relative standard error, RSE, in percent). We see that the uncertainty is generally higher with the LOQ evaluations (as expected). We also see that the predictions of uncertainty are significantly larger than the D6 method. This too is expected, because the D2 method ignores design points where the model PRED is below LOQ (the last observation in the design), whereas it appears from the previous figure that ~25% of the observations from the last design point will be above LOQ. The M6 method accounts for this probability that the last design point will have data above LOQ and is thus a more realistic assessment of the expected parameter uncertainty.

Parameter No LOQ D6 D2
CL 5 6 6
V 4 4 4
KA 15 17 15
d_CL 34 50 498
d_V 70 109 428
d_KA 28 33 113
sig_prop 89 161 1444
sig_add 36 118 2127

ULOQ handling

If needed we can also handle upper limits of quantification. Lets assume we have an ULOQ at 7 units in addition to the LLOQ of 2 units:

library(ggplot2)
plot_model_prediction(poped_db, model_num_points = 500,facet_scales = "free",
                      PI=T, PI_alpha = 0.1) + 
  geom_hline(yintercept = 2,color="red",linetype="dotted",linewidth=1) + 
  geom_hline(yintercept = 7,color="blue",linetype="dotted",linewidth=1)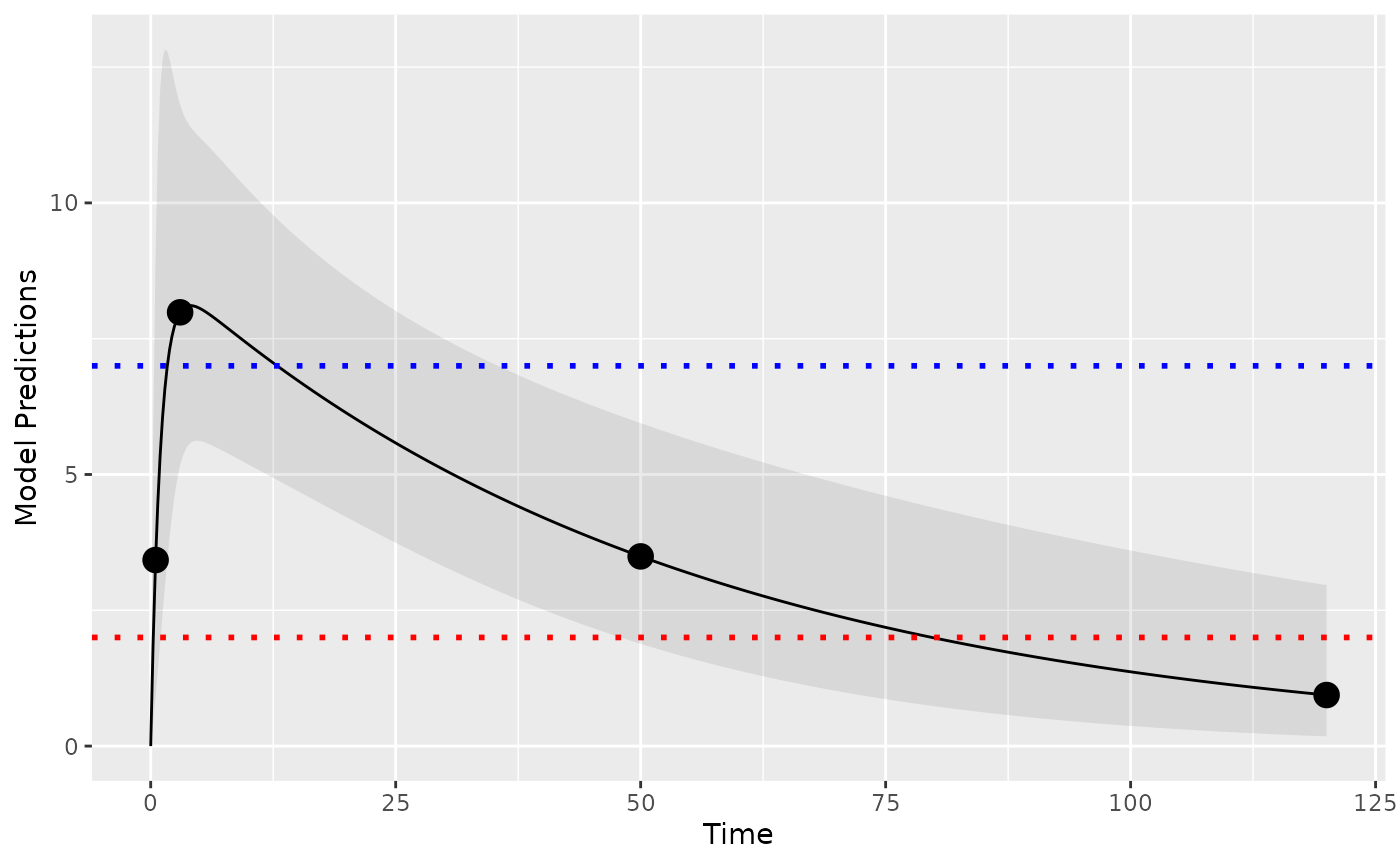

We can then evaluate the design based on the D2 and D6 methods.

eval_ul_D6 <-evaluate_design(poped_db,
                loq=2,
                uloq=7)

eval_ul_D2 <- evaluate_design(poped_db,
                                loq=2,
                                loq_method=2,
                                uloq=7,
                                uloq_method=2)
#> Problems inverting the matrix. Results could be misleading.

And then look at the predicted RSE in percent.

eval_rse_2 <-
  tibble::tibble("Parameter"=names(eval_full$rse),
                 "No LOQ"=round(eval_full$rse),
                 "D6 (only LLOQ)"=round(eval_D6$rse),
                 "D2 (only LLOQ)"=round(eval_D2$rse),
                 "D6 (ULOQ and LLOQ)"=round(eval_ul_D6$rse),
                 "D2 (ULOQ and LLOQ)"=round(eval_ul_D2$rse))
eval_rse_2
Parameter No LOQ D6 (only LLOQ) D2 (only LLOQ) D6 (ULOQ and LLOQ) D2 (ULOQ and LLOQ)
CL 5 6 6 6 6
V 4 4 4 8 0
KA 15 17 15 21 14
d_CL 34 50 498 59 276
d_V 70 109 428 203 1743
d_KA 28 33 113 35 55
sig_prop 89 161 1444 297 1645
sig_add 36 118 2127 122 6

Design optimization

Next, we optimize the design using the different methods of computing the FIM. Here we optimize only using the lower LOQ.

optim_D6 <- poped_optim(poped_db, opt_xt = TRUE,
                        parallel=T,
                        loq=2)

optim_D2 <- poped_optim(poped_db, opt_xt = TRUE,
                        parallel=T,
                        loq=2,
                        loq_method=2)

optim_full <- poped_optim(poped_db, opt_xt = TRUE,
                        parallel=T)

All designs points shown together in one plot to demonstrate how the different handling of BLQ data results in different optimal designs. The “full” design, ignoring LOQ, places a design point at the end of the sampling space, which will results in many observations below LOQ. Both the D2 and D6 methods push the design points to regions where fewer LOQ observations will occur.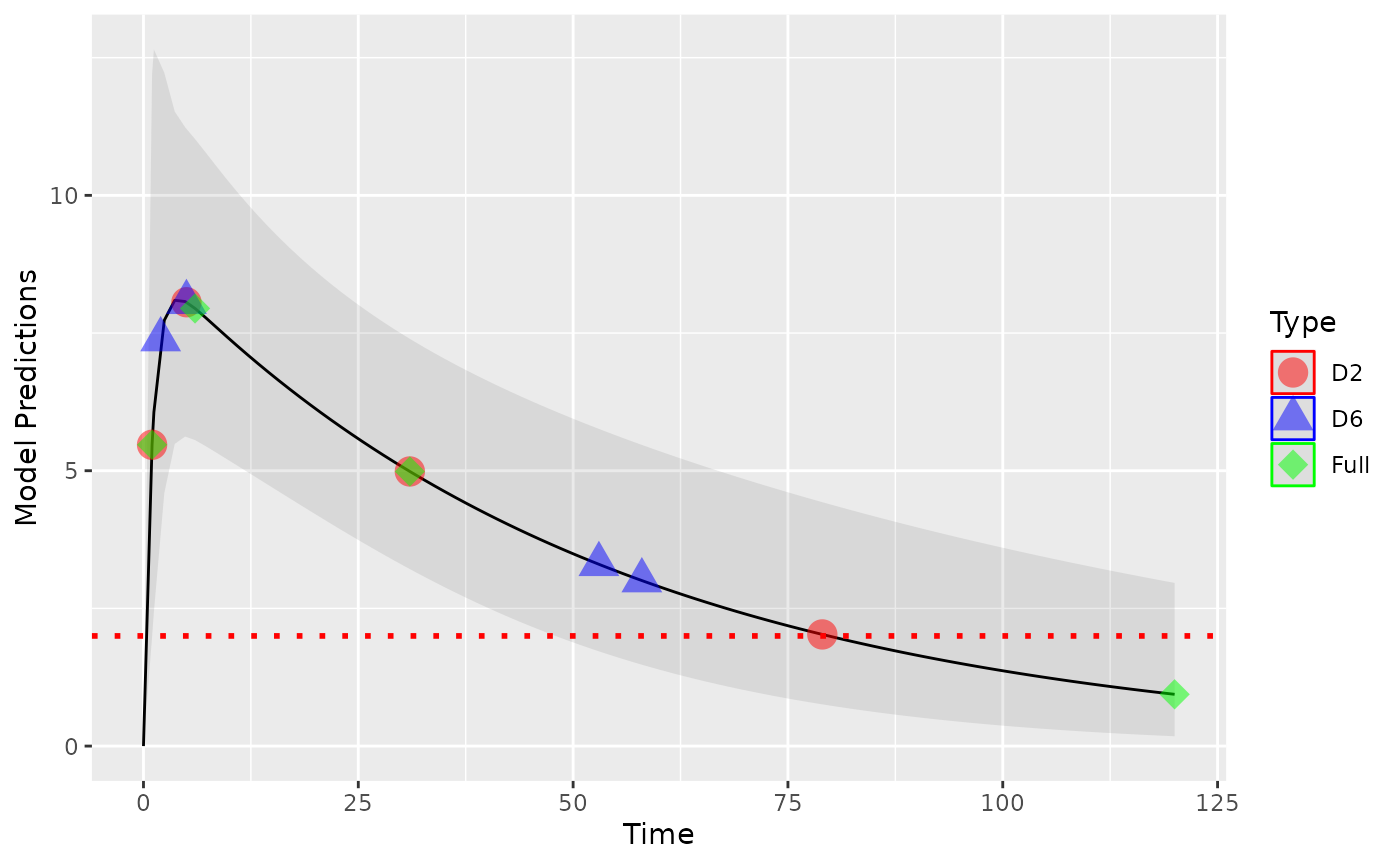

To compare the effects of these different designs on parameter precision, we evaluate each of the optimal designs above using the D6 method.

optim_full_D6<- with(optim_full, 
  evaluate_design(poped.db,
                  loq=2))

optim_D2_D6<- with(optim_D2, 
  evaluate_design(poped.db,
                  loq=2))

optim_D6_D6<- with(optim_D6, 
  evaluate_design(poped.db,
                  loq=2))

The expected %RSE of the parameters is shown below. We see that the D6 optimized design gives, on average, the best parameter precision. The D2 optimal design stragetgy may be a reasonable obtain designs that are “good enough” if the D6 method is too slow for optimization.

optim_rse_D6 <-
  tibble::tibble("Parameter"=names(eval_full$rse),
                 "No LOQ"=round(optim_full_D6$rse),
                 "D6"=round(optim_D6_D6$rse),
                 "D2"=round(optim_D2_D6$rse))
optim_rse_D6
Parameter No LOQ D6 D2
CL 7 5 6
V 4 3 3
KA 16 17 16
d_CL 67 34 43
d_V 58 54 52
d_KA 30 39 30
sig_prop 114 96 93
sig_add 152 60 92

References

Nyberg, Joakim, Caroline Bazzoli, Kay Ogungbenro, Alexander Aliev, Sergei Leonov, Stephen Duffull, Andrew C Hooker, and France Mentré. 2015. “Methods and software tools for design evaluation in population pharmacokinetics-pharmacodynamics studies.” British Journal of Clinical Pharmacology 79 (1): 6–17. https://doi.org/10.1111/bcp.12352.
Nyberg, Joakim, Sebastian Ueckert, Eric A. Strömberg, Stefanie Hennig, Mats O. Karlsson, and Andrew C. Hooker. 2012. “PopED: An extended, parallelized, nonlinear mixed effects models optimal design tool.” Computer Methods and Programs in Biomedicine 108 (2): 789–805. https://doi.org/10.1016/j.cmpb.2012.05.005.
Vong, Camille, Sebastian Ueckert, Joakim Nyberg, and Andrew C. Hooker. 2012. “Handling Below Limit of Quantification Data in Optimal Trial Design.” PAGE, Abstracts of the Annual Meeting of the Population Approach Group in Europe. https://www.page-meeting.org/?abstract=2578.

Version information 

sessionInfo()
#> R version 4.4.1 (2024-06-14)
#> Platform: x86_64-pc-linux-gnu
#> Running under: Ubuntu 22.04.5 LTS
#> 
#> Matrix products: default
#> BLAS:   /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3 
#> LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.20.so;  LAPACK version 3.10.0
#> 
#> locale:
#>  [1] LC_CTYPE=C.UTF-8       LC_NUMERIC=C           LC_TIME=C.UTF-8       
#>  [4] LC_COLLATE=C.UTF-8     LC_MONETARY=C.UTF-8    LC_MESSAGES=C.UTF-8   
#>  [7] LC_PAPER=C.UTF-8       LC_NAME=C              LC_ADDRESS=C          
#> [10] LC_TELEPHONE=C         LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C   
#> 
#> time zone: UTC
#> tzcode source: system (glibc)
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#> [1] PopED_0.7.0      kableExtra_1.4.0 knitr_1.48       ggplot2_3.5.1   
#> 
#> loaded via a namespace (and not attached):
#>  [1] sass_0.4.9        utf8_1.2.4        generics_0.1.3    xml2_1.3.6       
#>  [5] gtools_3.9.5      stringi_1.8.4     digest_0.6.37     magrittr_2.0.3   
#>  [9] evaluate_1.0.0    grid_4.4.1        pkgload_1.4.0     mvtnorm_1.3-1    
#> [13] fastmap_1.2.0     rprojroot_2.0.4   jsonlite_1.8.9    brio_1.1.5       
#> [17] fansi_1.0.6       viridisLite_0.4.2 scales_1.3.0      codetools_0.2-20 
#> [21] textshaping_0.4.0 jquerylib_0.1.4   cli_3.6.3         rlang_1.1.4      
#> [25] munsell_0.5.1     withr_3.0.1       cachem_1.1.0      yaml_2.3.10      
#> [29] tools_4.4.1       dplyr_1.1.4       colorspace_2.1-1  vctrs_0.6.5      
#> [33] R6_2.5.1          lifecycle_1.0.4   stringr_1.5.1     fs_1.6.4         
#> [37] htmlwidgets_1.6.4 ragg_1.3.3        pkgconfig_2.0.3   desc_1.4.3       
#> [41] pkgdown_2.1.1     pillar_1.9.0      bslib_0.8.0       gtable_0.3.5     
#> [45] glue_1.8.0        systemfonts_1.1.0 xfun_0.48         tibble_3.2.1     
#> [49] tidyselect_1.2.1  highr_0.11        rstudioapi_0.16.0 farver_2.1.2     
#> [53] htmltools_0.5.8.1 rmarkdown_2.28    svglite_2.1.3     labeling_0.4.3   
#> [57] testthat_3.2.1.1  compiler_4.4.1