Plot the efficiency of windows

Function plots the efficiency of windows around the sample time points. The function samples from a uniform distribution around the sample time points for each group (or each individual with deviate_by_id=TRUE, with slower calculation times) and compares the results with the design defined in poped.db. The maximal and minimal allowed values for all design variables as defined in poped.db are respected (e.g. poped.db$design_space$minxt and poped.db$design_space$maxxt).

Usage

plot_efficiency_of_windows(
  poped.db,
  xt_windows = NULL,
  xt_plus = xt_windows,
  xt_minus = xt_windows,
  iNumSimulations = 100,
  y_eff = TRUE,
  y_rse = TRUE,
  ofv_calc_type = poped.db$settings$ofv_calc_type,
  mean_line = TRUE,
  mean_color = "red",
  deviate_by_id = FALSE,
  parallel = F,
  seed = round(runif(1, 0, 1e+07)),
  ...
)

Arguments

poped.db

A poped database

xt_windows

The distance on one direction from the optimal sample times. Can be a number or a matrix of the same size as the xt matrix found in poped.db$design$xt.

xt_plus

The upper distance from the optimal sample times (xt + xt_plus). Can be a number or a matrix of the same size as the xt matrix found in poped.db$design$xt.

xt_minus

The lower distance from the optimal sample times (xt - xt_minus). Can be a number or a matrix of the same size as the xt matrix found in poped.db$design$xt.

iNumSimulations

The number of design simulations to make within the specified windows.

y_eff

Should one of the plots created have efficiency on the y-axis?

y_rse

Should created plots include the relative standard error of each parameter as a value on the y-axis?

ofv_calc_type

OFV calculation type for FIM

1 = "D-optimality". Determinant of the FIM: det(FIM)
2 = "A-optimality". Inverse of the sum of the expected parameter variances: 1/trace_matrix(inv(FIM))
4 = "lnD-optimality". Natural logarithm of the determinant of the FIM: log(det(FIM))
6 = "Ds-optimality". Ratio of the Determinant of the FIM and the Determinant of the uninteresting rows and columns of the FIM: det(FIM)/det(FIM_u)
7 = Inverse of the sum of the expected parameter RSE: 1/sum(get_rse(FIM,poped.db,use_percent=FALSE))

mean_line

Should a mean value line be created?

mean_color

The color of the mean value line.

deviate_by_id

Should the computations look at deviations per individual instead of per group?

parallel

Should we use parallel computations (T/F)? Other options can be defined in this function and passed to start_parallel. See especially the options dlls and mrgsolve_model from that function if you have a model defined with compiled code or are using mrgsolve.

seed

The random seed to use.

...

Extra arguments passed to evaluate.fim

Value

A ggplot object.

Examples

library(PopED)

############# START #################
## Create PopED database
## (warfarin model for optimization)
#####################################

## Warfarin example from software comparison in:
## Nyberg et al., "Methods and software tools for design evaluation 
##   for population pharmacokinetics-pharmacodynamics studies", 
##   Br. J. Clin. Pharm., 2014. 

## Optimization using an additive + proportional reidual error  
## to avoid sample times at very low concentrations (time 0 or very late samples).

## find the parameters that are needed to define from the structural model
ff.PK.1.comp.oral.sd.CL
#> function (model_switch, xt, parameters, poped.db) 
#> {
#>     with(as.list(parameters), {
#>         y = xt
#>         y = (DOSE * Favail * KA/(V * (KA - CL/V))) * (exp(-CL/V * 
#>             xt) - exp(-KA * xt))
#>         return(list(y = y, poped.db = poped.db))
#>     })
#> }
#> <bytecode: 0x557079188b38>
#> <environment: namespace:PopED>

## -- parameter definition function 
## -- names match parameters in function ff
sfg <- function(x,a,bpop,b,bocc){
  parameters=c(CL=bpop[1]*exp(b[1]),
               V=bpop[2]*exp(b[2]),
               KA=bpop[3]*exp(b[3]),
               Favail=bpop[4],
               DOSE=a[1])
  return(parameters) 
}

## -- Define initial design  and design space
poped.db <- create.poped.database(ff_fun=ff.PK.1.comp.oral.sd.CL,
                                  fg_fun=sfg,
                                  fError_fun=feps.add.prop,
                                  bpop=c(CL=0.15, V=8, KA=1.0, Favail=1), 
                                  notfixed_bpop=c(1,1,1,0),
                                  d=c(CL=0.07, V=0.02, KA=0.6), 
                                  sigma=c(prop=0.01,add=0.25),
                                  groupsize=32,
                                  xt=c( 0.5,1,2,6,24,36,72,120),
                                  minxt=0.01,
                                  maxxt=120,
                                  a=c(DOSE=70),
                                  mina=c(DOSE=0.01),
                                  maxa=c(DOSE=100))

############# END ###################
## Create PopED database
## (warfarin model for optimization)
#####################################




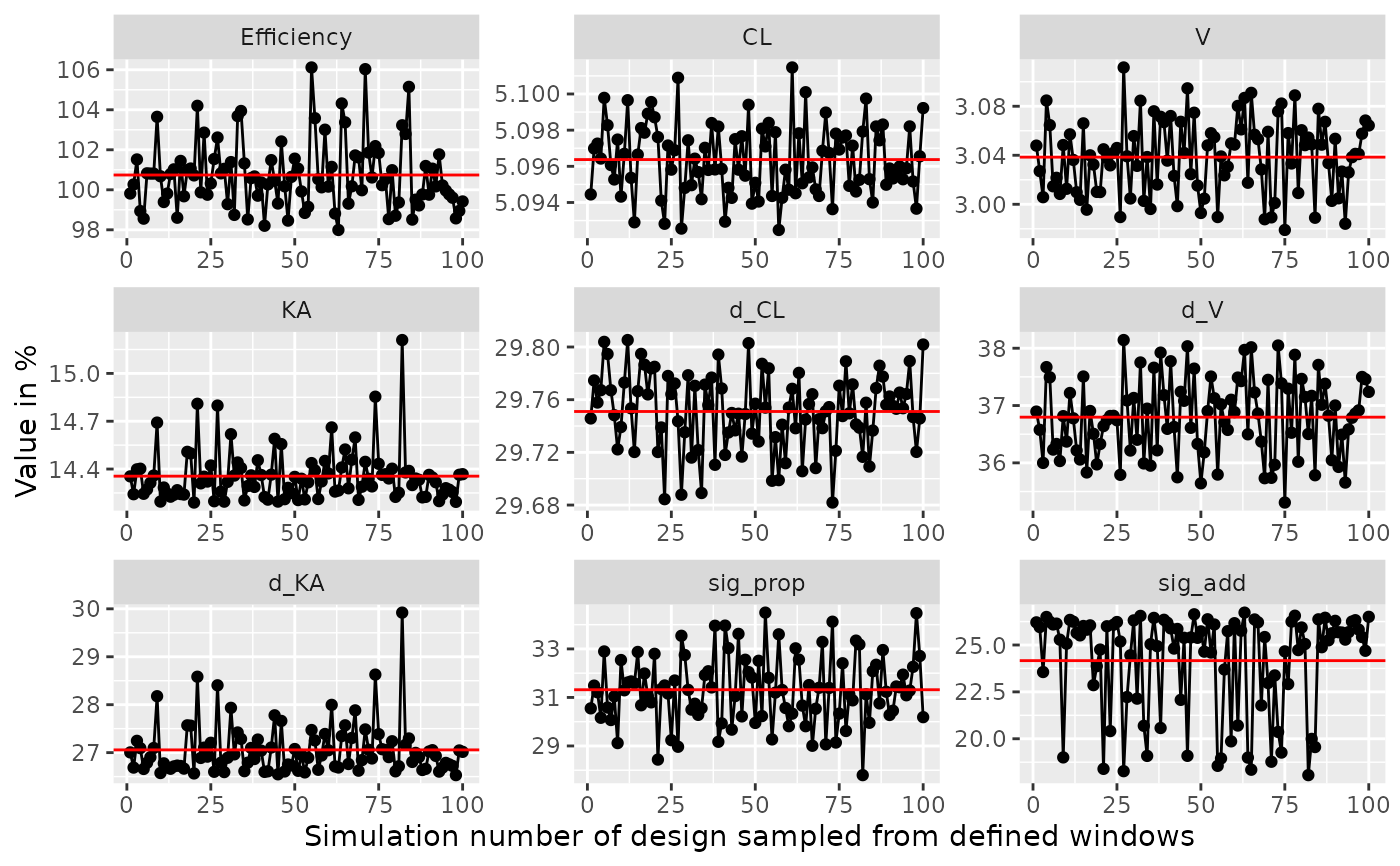
# Examine efficiency of sampling windows at plus/minus 0.5 hours from 
# sample points in the design
plot_efficiency_of_windows(poped.db,xt_windows=0.5)



if(interactive()){  

  plot_efficiency_of_windows(poped.db,
                             xt_plus=c( 0.5,1,2,1,2,3,7,1),
                             xt_minus=c( 0.1,2,5,4,2,3,6,2))
  
  plot_efficiency_of_windows(poped.db,xt_windows=c( 0.5,1,2,1,2,3,7,1))
  
  
  plot_efficiency_of_windows(poped.db,
                             xt_plus=c( 0.5,1,2,1,2,3,7,1),
                             xt_minus=c( 0.1,2,5,4,2,3,6,2),
                             y_rse=FALSE)
  
  plot_efficiency_of_windows(poped.db,
                             xt_plus=c( 0.5,1,2,1,2,3,7,1),
                             xt_minus=c( 0.1,2,5,4,2,3,6,2),
                             y_eff=FALSE)
}

Usage

Arguments

Value

See also

Examples