RUV model: Additive and Proportional.

This is a residual unexplained variability (RUV) model function that encodes the model described above. The function is suitable for input to the create.poped.database function using the fError_file argument.

Usage

feps.add.prop(model_switch, xt, parameters, epsi, poped.db)

Arguments

model_switch: a vector of values, the same size as xt, identifying which model response should be computed for the corresponding xt value. Used for multiple response models.
xt: a vector of independent variable values (often time).
parameters: A named list of parameter values.
epsi: A matrix with the same number of rows as the xt vector, columns match the numbers defined in this function.
poped.db: a poped database. This can be used to extract information that may be needed in the model file.

Value

A list consisting of:

y the values of the model at the specified points.
poped.db A (potentially modified) poped database.

Examples

library(PopED)

## find the parameters that are needed to define in the structural model
ff.PK.1.comp.oral.md.CL
#> function (model_switch, xt, parameters, poped.db) 
#> {
#>     with(as.list(parameters), {
#>         y = xt
#>         N = floor(xt/TAU) + 1
#>         y = (DOSE * Favail/V) * (KA/(KA - CL/V)) * (exp(-CL/V * 
#>             (xt - (N - 1) * TAU)) * (1 - exp(-N * CL/V * TAU))/(1 - 
#>             exp(-CL/V * TAU)) - exp(-KA * (xt - (N - 1) * TAU)) * 
#>             (1 - exp(-N * KA * TAU))/(1 - exp(-KA * TAU)))
#>         return(list(y = y, poped.db = poped.db))
#>     })
#> }
#> <bytecode: 0x557071c69eb0>
#> <environment: namespace:PopED>

## -- parameter definition function 
## -- names match parameters in function ff
sfg <- function(x,a,bpop,b,bocc){
  parameters=c( V=bpop[1]*exp(b[1]),
                KA=bpop[2]*exp(b[2]),
                CL=bpop[3]*exp(b[3]),
                Favail=bpop[4],
                DOSE=a[1],
                TAU=a[2])
  return( parameters ) 
}

## -- Define design and design space
poped.db <- create.poped.database(ff_fun=ff.PK.1.comp.oral.md.CL,
                                  fg_fun=sfg,
                                  fError_fun=feps.add.prop,
                                  groupsize=20,
                                  m=2,
                                  sigma=c(0.04,5e-6),
                                  bpop=c(V=72.8,KA=0.25,CL=3.75,Favail=0.9), 
                                  d=c(V=0.09,KA=0.09,CL=0.25^2), 
                                  notfixed_bpop=c(1,1,1,0),
                                  notfixed_sigma=c(0,0),
                                  xt=c( 1,2,8,240,245),
                                  minxt=c(0,0,0,240,240),
                                  maxxt=c(10,10,10,248,248),
                                  a=cbind(c(20,40),c(24,24)),
                                  bUseGrouped_xt=1,
                                  maxa=c(200,24),
                                  mina=c(0,24))

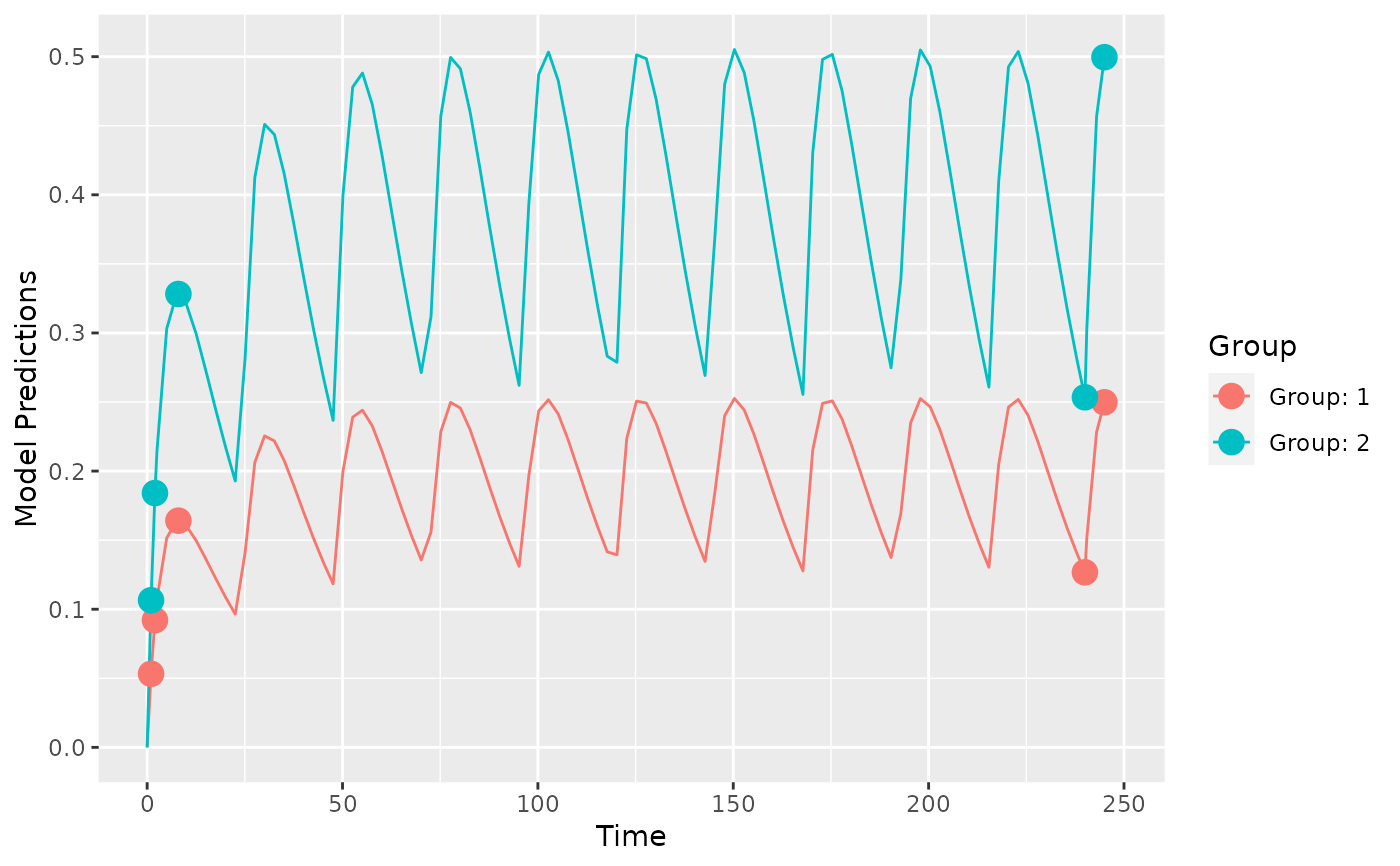
##  create plot of model without variability 
plot_model_prediction(poped.db)


## evaluate initial design
FIM <- evaluate.fim(poped.db) 
FIM
#>             [,1]        [,2]         [,3]       [,4]       [,5]        [,6]
#> [1,]  0.05336692   -8.683963  -0.05863412   0.000000   0.000000    0.000000
#> [2,] -8.68396266 2999.851007 -14.43058560   0.000000   0.000000    0.000000
#> [3,] -0.05863412  -14.430586  37.15243290   0.000000   0.000000    0.000000
#> [4,]  0.00000000    0.000000   0.00000000 999.953587 312.240246    3.202847
#> [5,]  0.00000000    0.000000   0.00000000 312.240246 439.412556    2.287838
#> [6,]  0.00000000    0.000000   0.00000000   3.202847   2.287838 3412.005199
det(FIM)
#> [1] 3.627987e+12
get_rse(FIM,poped.db)
#>         V        KA        CL       d_V      d_KA      d_CL 
#>  8.215338 10.090955  4.400304 39.833230 60.089601 27.391518

Usage

Arguments

Value

See also

Examples